Blender para perdidos en el espacio
El vector normal es un concepto geométrico que se utiliza en Blender y que tiene gran importancia para la mayoría de operaciones que realiza el programa. Dado un plano que tenga todos sus puntos en un espacio euclídeo de dos dimensiones existirían dos vectores normales, ambos en dirección perpendicular al plano pero en sentidos contrarios. Es como si nos imagináramos una hoja de papel sobre una mesa, el vector normal de la cara de la hoja que está hacia arriba apuntaría hacia el techo y el de la cara que está en contacto con la mesa apuntaría hacia el suelo, pero si damos la vuelta a la hoja los vectores normales cambiarían de sentido, es decir rotarían 180 grados. Si estuviéramos modelando esa hoja con Blender tendríamos que hacer saber al programa que lo que antes estaba abajo ahora está arriba, para eso se usa la herramienta de recalcular las normales.
En un espacio infinito como el que Blender pone a nuestra disposición, no están claros conceptos como dentro y fuera o arriba y abajo si no se referencian a algo. Por ejemplo, si queremos modelar un dado y el interior de una habitación en los dos casos partiríamos de un cubo, pero para el dado las normales apuntarían hacia fuera y para la habitación hacia dentro. Si las normales no están bien calculadas los resultados pueden no ser los esperados en muchas ocasiones, por ejemplo al aplicar el modificador booleano, o al hacer el renderizado ya que los cálculos que hará serán erroneos porque la referencia también es errónea, y puede que no de ningún error, simplemente el resultado no será el esperado y esto a veces desconcierta mucho. También es muy importante en la impresión 3D porque podría interpretarlo como un agujero en la malla y estropear la impresión del modelo.
Aunque las normales no forman parte de la estructura de la malla propiamente dicha, son necesarias para identificar las caras de una malla y afectan a muchas de las operaciones que se hacen con ella como ya hemos dicho, por ejemplo en el renderizado, o a la hora de aplicar las sombras a la malla. Con la herramienta de recalcular las normales de Blender, marcamos cual de los dos vectores normales de cada cara de la malla es el que tiene que usar como referencia para los cálculos. Una malla puede tener sus normales apuntando hacia dentro o hacia fuera pero lo normal es que todas sus caras tengan sus normales en el mismo sentido. Si en una misma malla hay caras con normales diferentes puede dar errores por ejemplo con el modificador booleano, que en este caso si que daría error.
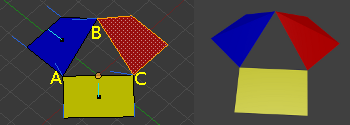
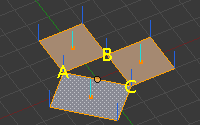Para definir una cara hacen falta al menos 3 vértices, pero no basta con tener la información de los vértices y de las aristas, el vector normal es el que realmente nos indica si existe una cara y su orientación. En la imagen vemos 3 vértices: A, B y C, y 3 aristas: AB, AC y BC, sin embargo no existe una cara formada por ABC. Las líneas azul claro representan las normales de las caras que como se ve apuntan las 3 en el mismo sentido, las líneas azul oscuro representan las normales de las vértices y se calculan en función de las normales de las caras adyacentes para aportar información extra.
Por defecto las normales no se ven en la representación de la malla en la ventana 3D pero se pueden hacer visibles desde el panel Mesh Properties que se encuentra entre la ventana 3D y la ventana Outliner (esquina superior derecha de la pantalla) y que si está oculto se hace visible pulsando la tecla N, en la pestaña Mesh Display. En esta pestaña podemos hacerlas visibles en la opción Normals pulsando en el cubo que tiene una cara seleccionada en color naranja, también se puede cambiar el tamaño. Cuando están visibles se muestran como una pequeña línea de color azul claro perpendicular a una de las dos caras de cada polígono de la malla. También se pueden mostrar las normales de los vértices. Si las hacemos visibles podemos darnos cuenta facilmente si hay alguna cara con la normal al revés y podremos corregir estos defectos y evitarnos sorpresas antes de que la malla se vaya haciendo más compleja y sea más difícil localizarlos.
En Blender hay una herramienta para mallas que permite recalcular las normales, se accede desde el menú Mesh en la opción Normals. Tiene 3 posibles acciones: recalcular hacia fuera (también podría pulsarse Control N), recalcular hacia dentro (Control Shift N) y voltear. También se pueden voltear desde el menú emergente Specials que aparece al pulsar la tecla W en la opción Flip Normals y funciona como un interruptor cambiando entre una normal y otra. Existe otra forma de voltear las normales de las caras desde el menú Mesh en la opción Faces (se puede llegar al mismo sitio pulsando Control F) y una vez aquí elegir la opción Flip Normals. Sea la que sea la forma que usemos para recalcular las normales, tendremos que tener previamente seleccionadas las caras que queramos recalcular. Desde el Modo Edición, bien seleccionamos todo pulsando la tecla A, o con cualquier otro método de selección, seleccionaremos las caras que queramos que sean afectadas, ya que algunas veces esta forma de recalcular las normales no funciona como esperamos y hay que ir seleccionando las caras por grupos.
Blender utiliza la forma de la malla para poder calcular que cara apunta dentro y cual apunta fuera, pero existen algunas mallas en las que sólo por la forma esto no puede saberse facilmente y por eso se utilizan también otros métodos para calcularlo, como la posición del centro del objeto. Por ejemplo, esto puede ocurrir en mallas que no son cerradas, es decir que no tienen unidas todas sus aristas a dos caras, como un plano, donde no existe dentro ni fuera, si existen aristas que no pertenecen exactamente a dos caras, se denominan mallas Non-manifold, en las que algunas de sus aristas pueden estar unidas a una, a tres o a más caras. Aunque las mallas sean cerradas, puede haber problemas en caras que no tengan todos sus vértices en el mismo plano. También mallas mal construidas con geometría redundante (vértices duplicados) o sucias (con geometría dentro de la malla, por malas extrusiones por ejemplo) pueden dar problemas. Por todo esto, a veces hay que arreglar las normales a mano y no funciona recalcular todas, no es que el programa tenga un error, es que como la información no es completa los resultados no son los esperados. Veamos un ejemplo.
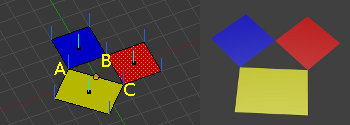Partimos de la misma malla usada en Definir una cara en la que tenemos tres caras de cuatro lados con todos sus vértices en el mismo plano, es decir, tienen el mismo valor para una de las coordenadas, en este ejemplo cero en el eje Z. Entre las tres caras hay un hueco definido por los vértices A, B y C. En este caso todas las normales están en el mismo sentido y no se aprecia en el renderizado gran diferencia con la siguiente imagen.
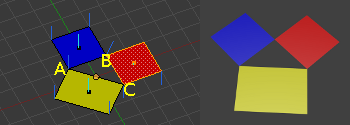En el ejemplo de esta imagen hemos volteado las normales de la cara roja, con lo que también se han volteado las normales de sus vértices, pero el resultado del render es similar a la imagen anterior, no se aprecian artefactos extraños ni rayas. Esto ocurre porque al igual que en la primera imagen, todos los puntos de la malla están en el mismo plano y es fácil calcular las normales.
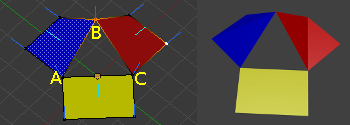En este caso hemos cambiado el valor de la coordenada Z a dos unidades en el vértice B, el resto se dejan como estaba en la primera imagen del ejemplo caras en el mismo plano. Al mover el vértice B hemos provocado que las caras roja y azul no tengan todos sus vértices en el mismo plano, con lo que ya no es tan fácil calcular la normal. Se crean dos triángulos imaginarios en cada cara, como si se hiciera un doblez en la cara, aunque curiosamente no las divide de igual forma. Estas subdivisones se ven reflejadas en como compone la superficie de la malla durante el renderizado.
En esta imagen hemos volteado la normal de la cara roja y el resultado de la subdivisión en triángulos imaginários en el modo edición es el mismo: crea una línea imaginária entre el vértice A y su opuesto en la cara azul, y otra línea entre el vértice B y su opuesto en la cara roja, pero el resultado del render es diferente, porque las normales de la cara roja y sus vértices son diferentes.
El motivo de que internamente lo convierta a triángulos, es porque en un triángulo todos sus puntos siempre están en el mismo plano y aunque movamos uno de los vértices seguirán estando en el mismo plano, en otro distinto, pero todos en el mismo. Esto sirve para simplificar muchos los cálculos que hay que hacer, por ejemplo en como inciden los rayos de luz sobre la superficie de la malla. Hemos dividido la cara azul y la roja en dos triángulos cada una y hemos hecho dos render, cada uno con las normales de las caras rojas en distinto sentido. En la imagen se puede ver que no se aprecia diferencia entre ambos, es similar al ejemplo Caras en el mismo plano.
Comprobar a menudo todas las normales haciéndolas visibles y sobre todo después de subdividir la malla, antes de aplicar texturas o luces y de usar modificadores, especialmente el booleano y siempre que observemos comportamientos extraños al realizar cualquier operación con la malla, como por ejemplo pequeños artefactos y líneas negras o errores en el renderizado.
Mantener la topología de la malla lo más límpia posible, eliminando la geometría innecesaria, duplicada o sucia, intentando que cada arista esté unida unicamente a dos caras, ni a más ni a menos, ya que las mallas que no cumplen estos requisitos dan muchos problemas no sólo con las normales, también con modificadores como el diezmador que no puede usarse.